Activités réseaux sociaux

Partie 1 : Recherche sur le réseau social (1h)

Choisir un seul réseau social.

• Principe de fonctionnement :
  • Quel est le principe de ce réseau social (comment les utilisateurs interagissent, quels types de contenus sont partagés) ?
• Nombre d’abonnés :
  • Trouvez le nombre actuel d’utilisateur à ce réseau social.
  • Est-ce que ce nombre est en hausse, en baisse ou stable (dynamique de croissance) ?
• Questions sur la vie privée et la sécurité :
  1. Les utilisateurs peuvent-ils régler des paramètres de confidentialité pour protéger leur vie privée ? Ces paramètres sont-ils facilement accessibles ?
  2. Est-il facile de se désinscrire de ce réseau social ?
  3. Le réseau propose-t-il une procédure pour obtenir une copie des données récoltées sur un utilisateur ? Si oui, est-elle simple à mettre en œuvre ?
  4. Le réseau efface-t-il toutes les données personnelles d’un utilisateur désinscrit ?
  5. Rechercher sur internet comment fonctionne une base de donnée, décrire son utilisation.
  6. L’utilisateur peut-il voir ce qu’il y a dans la base de donnée des GAFAM ? est-ce que toutes ses données personnelles sont alors réellement effacées ? Que dis la lois ?

Sécurité des données et risques de piratage :

1. Les données des utilisateurs sont-elles bien protégées sur ce réseau social ?
   • Quels types de mesures de sécurité sont mis en place pour protéger les données des utilisateurs ?
2. Ce réseau social a-t-il déjà été victime de fuites de données ou de piratages ?
   • Si oui, quels types de données ont été volés, et quelles ont été les conséquences pour les utilisateurs ?
   • Quelle réaction le réseau social a-t-il eu face à ces incidents ?
3. Comment le réseau social gère-t-il les données sensibles ?

Fonctionnement des algorithmes :

1. Comment fonctionne l’algorithme de recommandation de ce réseau social ?
   • Quels types de données sont utilisés pour proposer du contenu personnalisé aux utilisateurs (historique de navigation, interactions, etc.) ?
2. Quelles sont les conséquences de l’utilisation des algorithmes sur les utilisateurs ?
   • En quoi l’algorithme peut-il influencer la manière dont les utilisateurs interagissent avec le réseau social (temps passé, polarisation des idées, écho de leurs propres opinions, etc.) ?
3. Les utilisateurs ont-ils la possibilité de modifier les paramètres des algorithmes ?
   • Par exemple, peuvent-ils choisir de ne plus voir de publicités ciblées ou d’avoir un fil d’actualité non personnalisé ?

Monétisation et publicité :

1. Comment ce réseau social utilise-t-il les données des utilisateurs pour générer des revenus via la publicité ?
   • Les publicités sont-elles ciblées en fonction des informations collectées sur les utilisateurs ?
2. Ce réseau social propose-t-il des options payantes pour les utilisateurs ?
   • Si oui, quelles sont les fonctionnalités premium disponibles, et ces options offrent-elles des avantages en termes de confidentialité ou d’expérience utilisateur ?
3. Quelles entreprises ou industries sont les principaux annonceurs sur ce réseau social ?
   • Y a-t-il des secteurs spécifiques (mode, technologie, jeux vidéo, etc.) qui investissent massivement dans la publicité sur cette plateforme ?

Impact sociétal :

1. Quel rôle joue ce réseau social dans la diffusion de l’information ?
2. Quelle influence ce réseau social a-t-il sur la santé mentale de ses utilisateurs ?

Les Réseaux sociaux et graphes

Imaginez un réseau social ayant 6 abonnés (A, B, C, D, E et F) où :

• A est ami avec B, C et D
• B est ami avec A et D
• C est ami avec A, E et D
• D est ami avec tous les autres abonnés
• E est ami avec C, D et F
• F est ami avec E et D

La description de ce réseau social, malgré son faible nombre d’abonnés, est déjà quelque peu rébarbative, alors imaginez cette même description avec un réseau social comportant des millions d’abonnés !

Il existe un moyen plus « visuel » pour représenter ce réseau social : on peut représenter chaque abonné par un cercle (avec le nom de l’abonné situé dans le cercle) et chaque relation « X est ami avec Y » par un segment de droite reliant X et Y (« X est ami avec Y » et « Y est ami avec X » étant représenté par le même segment de droite).

Voici ce que cela donne avec le réseau social décrit ci-dessus :

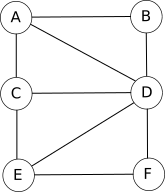
Ce genre de figure s’appelle un graphe. Les graphes sont des objets mathématiques très utilisés, notamment en informatique. Les cercles sont appelés des sommets et les segments de droites des arêtes.

Construisez un graphe de réseau social à partir des informations suivantes :

• A est ami avec B et E
• B est ami avec A et C
• C est ami avec B,F et D
• D est ami avec C,F et E
• E est ami avec A,D et F
• F est ami avec C, D et E

Voici quelques définitions sur les graphes :

chaîne : Dans un graphe, une chaîne reliant un sommet x à un sommet y est définie par une suite finie d’arêtes consécutives, reliant x à y.

exemple : Dans le graphe donné ci-dessus (graphe 1), A-D-E-C est une chaîne

distance entre 2 sommets : La distance entre deux sommets d’un graphe est le nombre minimum d’arêtes d’une chaîne allant de l’un à l’autre.

exemple : La distance entre le sommet A (graphe 1) et le sommet F est de 2 (chaîne A-D-F). ATTENTION : on parle bien du nombre minimum d’arêtes, A-D-E-F est aussi une chaîne entre A et F mais dans ce cas, nous avons 3 arêtes.

écartement : L’écartement d’un sommet est la distance maximale existant entre ce sommet et les autres sommets du graphe.

exemple 1 : Toujours dans le graphe 1 : distance (A-B) = 1 ; distance (A-C) = 1 ; distance (A-D) = 1 ; distance (A-E) = 2 ; distance (A-F) = 2 ; nous pouvons donc dire que la distance maximale existant entre le sommet A et les autres sommets du graphe est de 2 (distance (A-E) et distance (A-F)). Nous pouvons donc dire que l’écartement de A est de 2.

exemple 2 : distance (D-A) = 1 ; distance (D-B) = 1 ; distance (D-C) = 1 ; distance (D-E) = 1 ; distance (D-F) = 1 ; nous pouvons donc dire que l’écartement de D est de 1.

centre : On appelle centre d’un graphe, le sommet d’écartement minimal (le centre n’est pas nécessairement unique).

exemple : Dans le graphe 1 tous les sommets ont un écartement de 2 à l’exception du sommet D qui a un écartement de 1, nous pouvons donc affirmer que le centre du graphe 1 est le sommet D

rayon : On appelle rayon d’un graphe G, l’écartement d’un centre de G.

exemple : D a un écartement de 1, c’est le centre du graphe 1, nous pouvons donc dire que le rayon du graphe 1 est de 1.

diamètre : On appelle diamètre d’un graphe G, la distance maximale entre deux sommets du graphe G.

exemple : Dans le graphe 1 la distance maximale entre 2 sommets est de 2, nous pouvons donc dire que le diamètre du graphe est de 2.

Soit le graphe suivant :

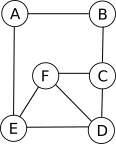
Déterminez le (ou les) centre(s) du graphe 2, en déduire le rayon du graphe 2. Déterminez le diamètre du graphe 2.

Experience de Milgram

En vous aidant de la vidéo ci-dessous, expliquez la notion de « petit monde » (expérience de Milgram en 1967 et étude de l’université de Milan en 2011)

Rendre le travail:

https://filerequest.stockageenligne.com/index.php/s/ezLMsnZfXT8yQyt